こんにちは、エンジニアインターンの南条です！

今回も前回(SHA256をGolangで実装する)に引き続きBitcoinで使われているハッシュ関数の一つであるRIPEMD-160を学ぶためにGolangでフルスクラッチで実装してみたいと思います！

あくまでも、仕組みを理解するためのコーディングなので、処理速度などは考慮せずに進めていきたいと思います。
コードについてのご指摘やアドバイスなどはTwitter(@nandehu0323)にいただけると非常にありがたいです！

RIPEMD
- RIPEMD-160
記号と演算子
各関数の作成
Padding
Parse
圧縮処理
Sum関数
出力結果
まとめ
Tip us!
参考文献

RIPEMD

RIPEMDはMD4の設計原理に基づいたものであり、SHA-1と同程度パフォーマンスを有している。
SHA-1[1]やSHA-2[2]がNSA[3]によって開発されたのと対照的に、RIPEMDはオープンな学術コミュニティによって開発され、特許による制限を受けない。(引用:Wikipedia)

RIPEMD-160

RIPEMD-160とは、RIPEMDの中でもハッシュ長が160ビット(20バイト)のものを指している。
ビットコインのブロックチェーンでもSHA-256と共に重要な役割を果たしている。

RIPEMDの大まかな説明はこんな感じです！
では、早速コーディングに移っていきたいと思います！

記号と演算子

今回RIPEMD-160を実装していくにあたって、【RIPEMD-160: A Strengthened Version of RIPEMD】[4]を参考に進めていくのですが、そこで使われる記号と演算子について軽く説明しておきます。

記号	意味	例
$lor$	論理和(OR)	1011 $lor$ 1100 = 1111
$land$	論理積(AND)	1011 $land$ 1100 = 1000
$oplus$	排他的論理和(XOR)	1011 $oplus$ 1100 = 0111
$lnot$	否定(NOT)	$lnot$ 1011 = 0100
x $ll$ n	左シフト(xをnビット左にシフトする)	1011 $ll$ 2 = 101100
x $gg$ n	右シフト(xをnビット右にシフトする)	1011 $gg$ 2 = 10

// ROTL ...
func ROTL(x uint32, n uint) uint32 {
    return (x << n) | (x >> (32 - n))
}

各関数の作成

まずはじめに、hashを計算するにあたって使用する関数を作成していきます！
RIPEMD-160の計算ではラウンドごとに決められた関数を用いて計算します。

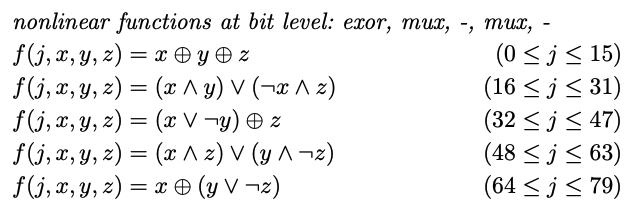
Nonlinear Functions
引用元:[RIPEMD-160:A Strengthened Version of RIPEMD]

// F ...
func f(j, x, y, z uint32) uint32 {
    if 0 <= j && j <= 15 {
        return x ^ y ^ z
    } else if 16 <= j && j <= 31 {
        return (x & y) | ((^x) & z)
    } else if 32 <= j && j <= 47 {
        return (x | (^y)) ^ z
    } else if 48 <= j && j <= 63 {
        return (x & z) | (y & (^z))
    } else if 64 <= j && j <= 79 {
        return x ^ (y | (^z))
    }
    return 0
}

Padding

次にパディングというデータの長さを整える処理をおこなっていきます。
冒頭で述べたようにRIPEMD関数はMD4関数の設計原理に基づき開発されました。
従って、これからおこなうPadding処理はMD4関数で行われるものと同様のものとなっていますので、
既知の方は読み飛ばしていただいて構いません。

RIPEMD-160では、ハッシュ化するメッセージ長が512ビット(64バイト)の倍数になっていなくてはなりません。したがって足りないデータを補うためにこのパディングという処理を行います。

パディング処理ではあるメッセージMの長さをl(エル)とし

を満たすkを用いて表された以下の形式のデータを末尾に追加する処理です。

メッセージの後ろにビットの”1”を加え0で埋め、残り64ビットにメッセージの長さl(エル)を加えます。

ここで注意点なのですが、前回のSHA-256の実装では残り64ビットにメッセージ長l(エル)を加える際にビックエンディアンで追加したのですが、今回のRIPEMD-160ではリトルエンディアンで追加しなければなりません。

バイトオーダーに関しましては下記の画像がわかりやすいと思います！

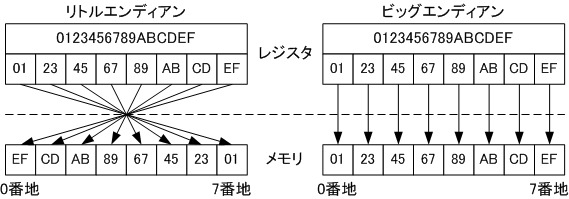
Difference of Byte-Order
引用元:バイトオーダ - ビッグエンディアン/リトルエディアン

こちらがそのコードになります。

// Padding ...
func Padding(message []byte) []byte {
    l := len(message)
    if l%64 < 56 {
        newlen := l % 64
        message = append(message[:], []byte{0x80}...)
        zero := make([]byte, 56-(newlen+1))
        message = append(message[:], zero[:]...)
        ms := make([]byte, 8)
        binary.LittleEndian.PutUint64(ms, uint64(l*8))
        message = append(message[:], ms[:]...)
    } else {
        message = append(message[:], []byte{0x80}...)
        newlen := l%64 + 1
        zero := make([]byte, 120-newlen)
        message = append(message[:], zero[:]...)
        ms := make([]byte, 8)
        binary.LittleEndian.PutUint64(ms, uint64(l*8))
        message = append(message[:], ms[:]...)
    }
    return message
}

先ほど述べたようにSHA-256の時とは違いLittleEndianでメッセージ長を追加します。

// RIPEMD-160
binary.LittleEndian.PutUint64(ms, uint64(l*8))
message = append(message[:], ms[:]...)

// SHA-256
binary.BigEndian.PutUint64(ms, uint64(l*8))
message = append(message[:], ms[:]...)

Parse

次に512ビットの倍数長に整えられたメッセージブロックを32ビット16個のかたまりに分割します。

// Parse ...
func Parse(message []byte) [][16]uint32 {
    fmt.Println(message)
    M := make([][16]uint32, len(message)/64)
    fmt.Println(M)
    for i := 0; i < len(message)/64; i++ {
        for j := 0; j < 16; j++ {
            M[i][j] = uint32(message[64*i+j*4]) | uint32(message[64*i+j*4+1])<<8 | uint32(message[64*i+j*4+2])<<16 | uint32(message[64*i+j*4+3])<<24
        }
    }
    return M
}

こちらの処理においてもSHA-256と異なる箇所があります。
メッセージブロックに関してもLittleEndianでメッセージを格納していきます。

// RIPEMD-160
M[i][j] = uint32(message[64*i+j*4]) | uint32(message[64*i+j*4+1])<<8 | uint32(message[64*i+j*4+2])<<16 | uint32(message[64*i+j*4+3])<<24

//SHA-256
M[i][j] = uint32(message[64*i+j*4+3]) | uint32(message[64*i+j*4+2])<<8 | uint32(message[64*i+j*4+1])<<16 | uint32(message[64*i+j*4])<<24

圧縮処理

次に、メインの計算部分に入っていきます。
まず、初期値に32ビットの5つのワードを指定します。

// Initial Hash Value
var H = []uint32{
    0x67452301,
    0xefcdab89,
    0x98badcfe,
    0x10325476,
    0xc3d2e1f0,
}

この設定した初期値と、32ビット16個のかたまりに分割されたメッセージブロックを用いて計算していきます。
この圧縮処理はそれぞれ16ステップの5つの並列ラウンドで構成されています。
MD4では16ステップの3つのラウンドなので16*3の合計48ステップに対して、RIPEMD-160では16*5*2の合計160ステップの計算を行うこととなります。

まず初期値から、２つのコピーを作成します。

// 左ラウンド用
a := H[0]
b := H[1]
c := H[2]
d := H[3]
e := H[4]
// 右ラウンド用
_a := H[0]
_b := H[1]
_c := H[2]
_d := H[3]
_e := H[4]

作成された２つの初期値のコピーは、それぞれ別の処理を行い、最後にまとめられます。
各ステップでは、メッセージブロック16個のうちの一つと、他4つの値から新しい値を計算します。

// 1ステップの処理(左ラウンド)
T = ROTL(a+f(t, b, c, d)+m[r[t]]+K(t), s[t]) + e // m[r[t]] メッセージブロック
a = e
e = d
d = ROTL(c, 10)
c = b
b = T
// 1ステップの処理(右ラウンド)
T = ROTL(_a+f(79-t, _b, _c, _d)+m[_r[t]]+_K(t), _s[t]) + _e // m[r[t]] メッセージブロック
_a = _e
_e = _d
_d = ROTL(_c, 10)
_c = _b
_b = T

なお、シフト量や変化をつけるための定数に関してはあらかじめ決められています。そちらに関しましては今回のコードをご覧ください。
最後に、左側のラウンドの結果と右側のラウンドの結果を合わせることによってハッシュを計算しています。

T = H[1] + c + _d
H[1] = H[2] + d + _e
H[2] = H[3] + e + _a
H[3] = H[4] + a + _b
H[4] = H[0] + b + _c
H[0] = T

大まかな流れについては下図を見ていただけるわかると思います！

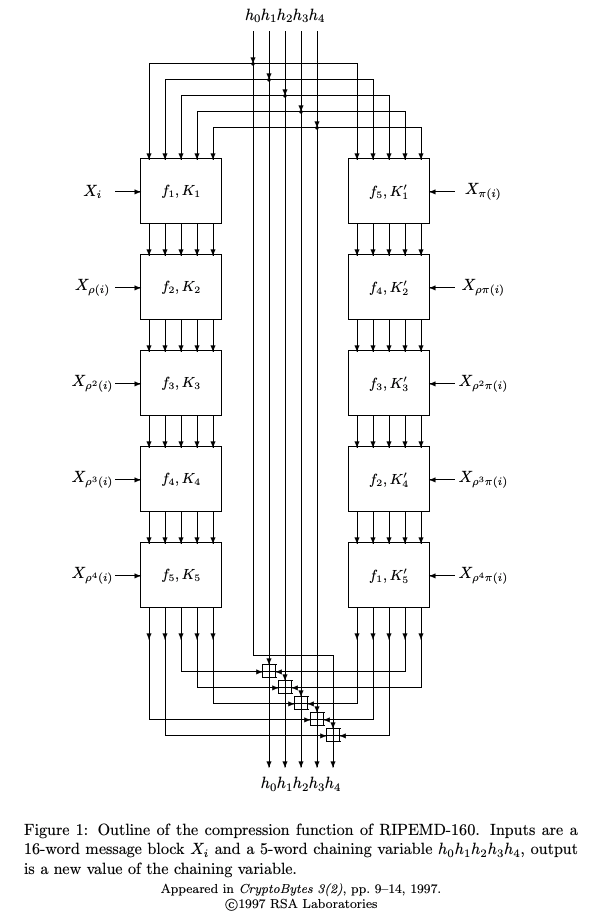
引用元:[RIPEMD-160:A Strengthened Version of RIPEMD]

ここまでの処理をまとめるとこのように表すことができます。

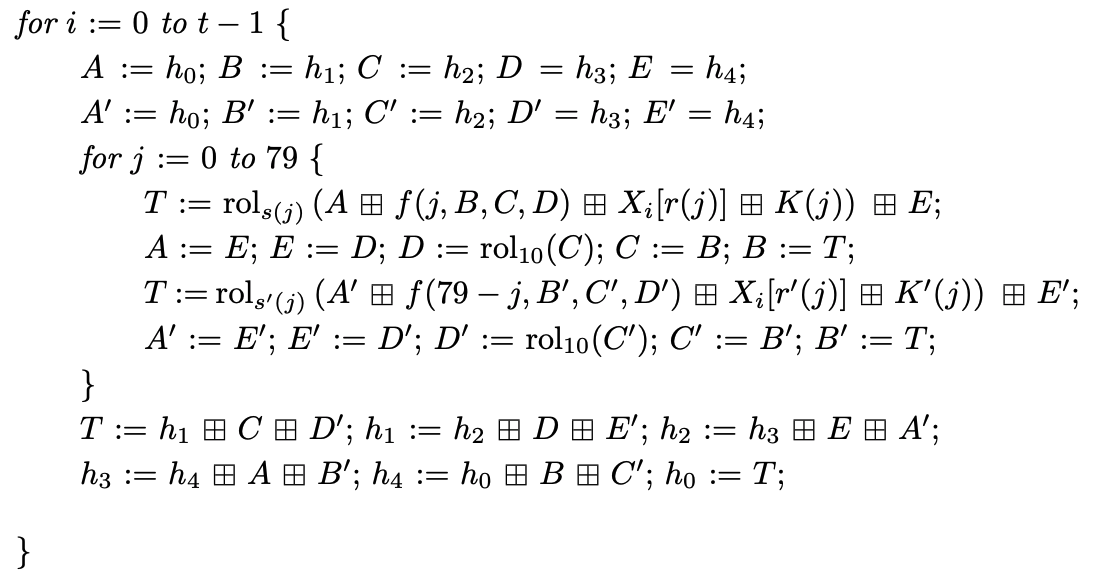
Pseudo-code
引用元:[RIPEMD-160:A Strengthened Version of RIPEMD]

上記の画像は擬似コードと呼ばれる、高級言語に似た架空の書式で書かれているので、これをコードに落とし込んでいきます。
こちらがそのコードになります。

// HashComp ...
func HashComp(M [][16]uint32) [20]byte {
    T := uint32(0)
    for _, m := range M {
        a := H[0]
        b := H[1]
        c := H[2]
        d := H[3]
        e := H[4]
        _a := H[0]
        _b := H[1]
        _c := H[2]
        _d := H[3]
        _e := H[4]
        for t := uint32(0); t < 80; t++ {
            T = ROTL(a+f(t, b, c, d)+m[r[t]]+K(t), s[t]) + e
            a = e
            e = d
            d = ROTL(c, 10)
            c = b
            b = T

            T = ROTL(_a+f(79-t, _b, _c, _d)+m[_r[t]]+_K(t), _s[t]) + _e
            _a = _e
            _e = _d
            _d = ROTL(_c, 10)
            _c = _b
            _b = T
        }
        T = H[1] + c + _d
        H[1] = H[2] + d + _e
        H[2] = H[3] + e + _a
        H[3] = H[4] + a + _b
        H[4] = H[0] + b + _c
        H[0] = T

    }
    var hash [20]byte
    for i, s := range H {
        hash[i*4] = byte(s)
        hash[i*4+1] = byte(s >> 8)
        hash[i*4+2] = byte(s >> 16)
        hash[i*4+3] = byte(s >> 24)
    }

    return hash
}

Sum関数

上記の一連の処理をまとめた関数を作成しました。

func Sum160(data []byte) [20]byte {
	padData := Padding(data)
	parsedData := Parse(padData)
	return HashComp(parsedData)
}

出力結果

今回は既存のライブラリである’crypto/ripemd160’を用いて検証を行いました。

func main() {
    data := []byte("abcdefg")
    fmt.Printf("RIPEMD-160 : %x\n", Sum160(data))
    rip := ripemd160.New()
    io.WriteString(rip, "abcdefg")
    fmt.Printf("RIPEMD-160 : %x\n", rip.Sum(nil))
}
> RIPEMD-160 : 874f9960c5d2b7a9b5fad383e1ba44719ebb743a
  RIPEMD-160 : 874f9960c5d2b7a9b5fad383e1ba44719ebb743a

まとめ

今回一からRIPEMD-160を実装してみて、ハッシュ関数によってバイトオーダーが異なった状態で処理したりだとか、それぞれのハッシュ関数の違いがより理解できたと思います。
またRIPEMD-160は、CRYPTRECの暗号リストにおいて運用監視暗号リストに含まれていて、互換性維持の目的以外での利用は推奨されていないにも関わらず、Bitcoinで使用されているのはなぜかと思い調べてみると、強衝突耐性がまだ破られていない一方向ハッシュの中で十分一意性が保たれていてかつ短いハッシュを生成できるゆえに使用されているということもわかりました。

今後もブロックチェーンを支えている技術の理論的なところをコードも交えて、紹介できたらなと思っています！

最後まで読んで頂きましてありがとうございました！

コード全体はGithub Gistに上がっています。

Twitter(@nandehu0323)もやっておりますのでぜひご感想やアドバイスお待ちしております！

Tip us!

エンジニアチームのブログを書くモチベーションが上がります 💪

address — 0xd6d478dCe4585a394834690158cf83581223C08f

RIPEMD160をGolangで実装する

Contents

RIPEMD

RIPEMD-160

記号と演算子

各関数の作成

Nonlinear Functions

Padding

Difference of Byte-Order

Parse

圧縮処理

Pseudo-code

Sum関数

出力結果

まとめ

Tip us!

0xd6d478dCe4585a394834690158cf83581223C08f

参考文献